Propriedades da adição – Cartaz e lembretes
Que bom ter você aqui!
Todos nós sabemos o que é adição.
Em resumo:
A adição é uma operação onde juntamos os elementos de dois os mais conjuntos, formando um novo conjunto. As propriedades da adição são: fechamento, comutatividade, associação e elemento neutro.
Vamos relembrar as propriedades da adição:
- Fechamento: Quando adicionamos dois ou mais números naturais, o resultado sempre será um número natural. Exemplo:8 + 6 = 14
- Comutativa: Podemos trocar a ordem das parcelas que o resultado não se altera. Exemplo: 4 + 2 = 6 e 2 + 4 = 6
- Elemento neutro: O zero adicionado a qualquer número natural não altera esse número. Por isso, o zero recebe o nome de elemento neutro. Exemplo: 4 + 0 = 4 e 0 + 4 = 4
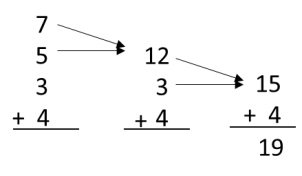
- Associativa: Na adição de números naturais, podemos associar as parcelas de diferentes formas que o resultado não se altera. Exemplo: 4 + 2 + 1 = 7
(4 + 2) +1 = ou 4 + (2 + 1) =
6 + 1 = 7 4 + 3 = 7
O professor deve salientar as aplicações práticas destas propriedades, particularmente a comutativa e a associativa. A primeira é usada com grande frequência como prova para verificar a exatidão dos resultados. A segunda é utilizada sempre que houver mais de duas parcelas:
Exemplo: 
Isto decorre do fato de ser a adição (como as demais operações) uma operação binária, isto é, ela envolve apenas dois termos – um operando e um operador – para obter um resultado.
É importante que o aluno entenda as propriedades da adição para poder avanças nas demais operações. Além disso, o conhecimento facilita a compreensão e realização de cálculos.
O post de hoje é um cartaz para a sala de aula e lembretes para colar no caderno dos alunos.
Falando um pouco sobre Adição
Em primeiro lugar, acredito que as etapas descritas a seguir já tenham sido superadas pelos alunos do 5º ano. No entanto, o uso eventual de Quadro Valor de Lugar (QVL) – veja aqui atividade de adição no QVL – servirá para consolidar os conceitos construídos, além de abrir horizontes para que o aluno estabeleça novas relações.
Por outro lado, caso algum aluno não tenha superado as referidas etapas, é conveniente parar o avanço do conteúdo e realizar atividades de revisão mais simples para facilitar a aprendizagem do aluno (rever pré-requisitos é sempre bom).
Todavia, sabemos que o conceito de adição é construído ao mesmo tempo que o conceito de números. A aprendizagem ocorre paralelemente.
Link de cartazes com os termos da adição e subtração:
Cartazes
Você também pode estar interessado em ver:
Matemática – SOS Professor Atividades
Cartazes com os termos da Multiplicação e da Divisão
Termos da adição e subtração – SOS Professor Atividades
Termos
Mais termos
Nos acompanhe também no nosso Pinterest vendo nossas atividades, e no blog em alguma atividade de seu interesse pesquise no “O que você procura?”
Amostras
Propriedades da adição – Cartaz e lembretes
Baixe o arquivo em PDF
Aviso de propriedade
Este material é totalmente gratuito e elaborado por @sosprofessoratividades.com.
Todas as atividades do blog/site são protegidas pela lei dos direitos autorais, nº 9.610/98 – proibido a venda, cópias para outros sites, blogs ou redes sociais.
Quer compartilhar? Compartilhe o link.
Obrigada♥
Propriedades da adição – Cartaz e lembretes (sosprofessoratividades.com)
Clique no quadro para baixar a atividade em PDF
Propriedades da adição – Cartaz e lembretes
ATENÇÃO!
Caso esteja baixando via celular, talvez seja necessário fazer
login em sua conta do Google.
Baixando através de um computador não é necessário fazer login.
Objetos de conhecimento:
Propriedades das operações para o desenvolvimento de diferentes estratégias de cálculo com números naturais.
Habilidade da BNCC:
(EF04MA05) Utilizar as propriedades das operações para desenvolver estratégias de cálculo.
