Olá amigos do Sosprofessoratividades!
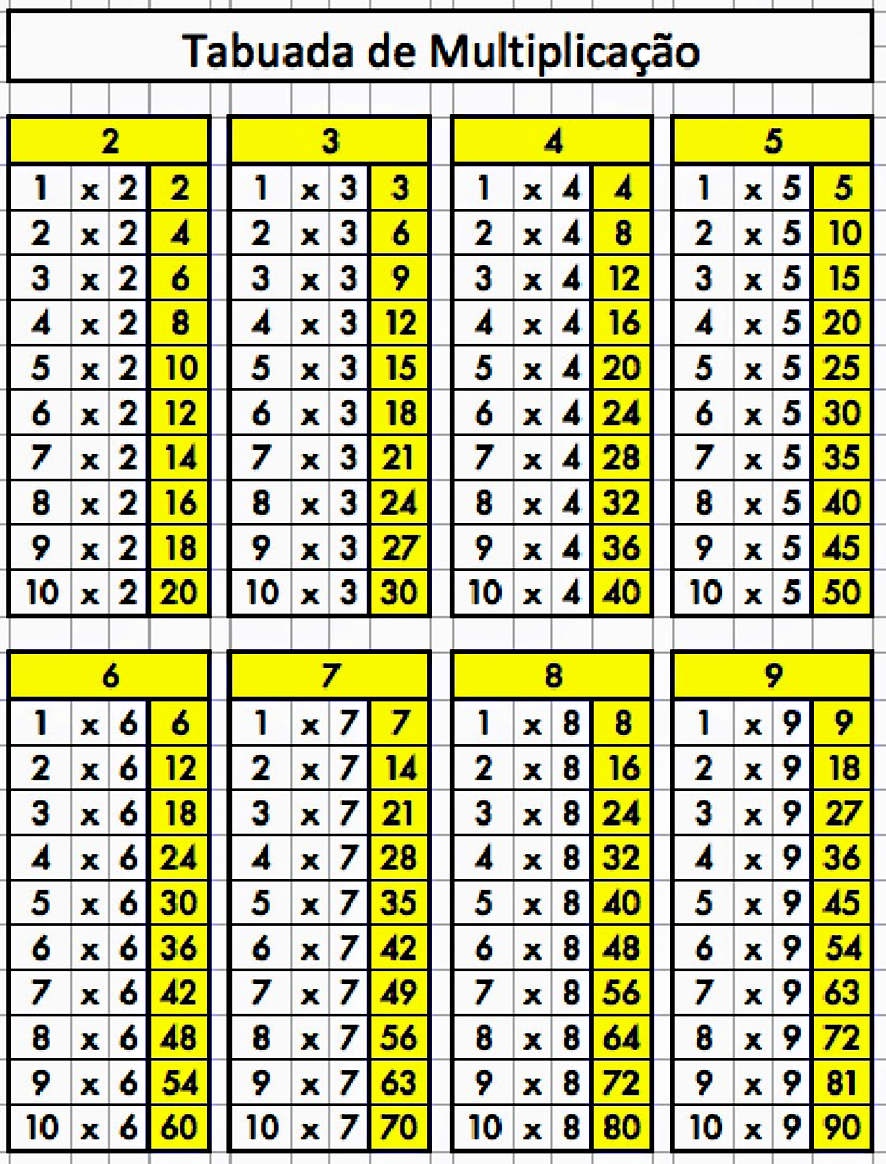
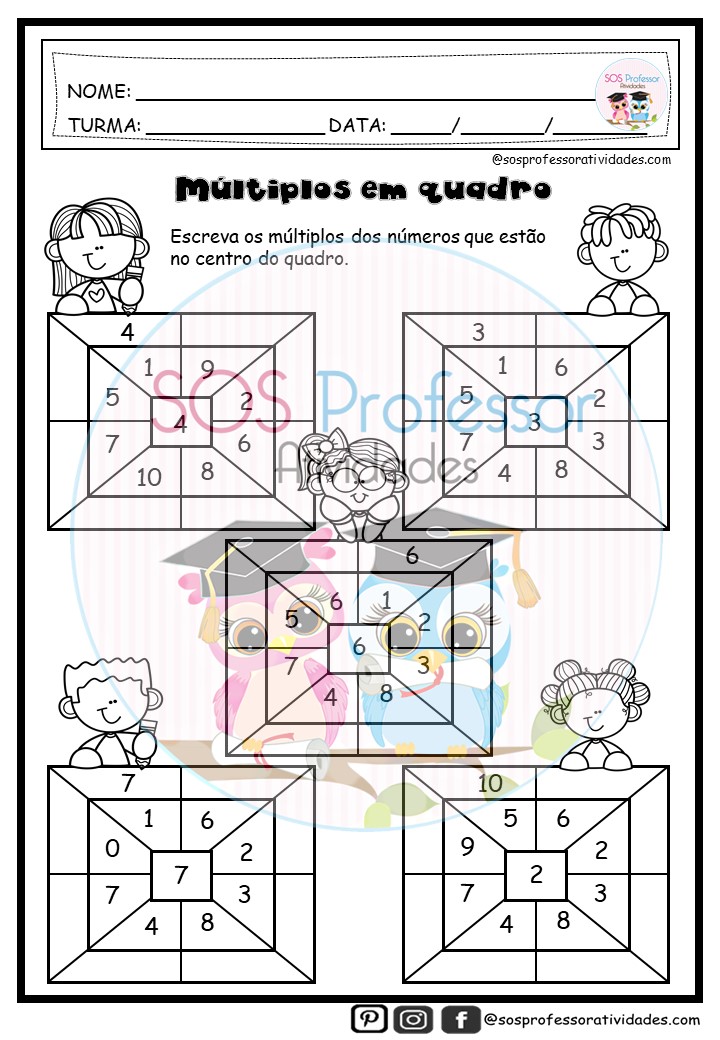
Tabuada 4º ano – Múltiplos em quadro
Tabuada 4º ano – uma forma lúdica de exercitar e memorizar a tabuada do 2, 3, 4, 6 e 7. O aluno irá completar o quadro com o produto da multiplicação do números contidos nele.
Você também pode estar interessado em ver:
Como ensinar multiplicação
O ensino da Tabuada no 4º ano é o salto do aprendizado de subtração e adição para o aprendizado de multiplicação é uma das tarefas mais assustadoras que os alunos enfrentarão na escola.
E não são apenas os alunos que têm problemas com o assunto.
Ao ensinar multiplicação, os educadores frequentemente começam com os conceitos errados ou passam pelas aulas muito rapidamente. Isso pode desencorajar e intimidar os alunos, prejudicando os resultados de aprendizagem.
Felizmente, existem estratégias conhecidas para evitar esses obstáculos.
Aprenda como introduzir conceitos-chave e como ensinar as crianças a aprender e memorizar a tabuada!
1. Relacione a multiplicação com a adição.
Evite começar com a memorização. Os alunos normalmente lutam para memorizar os fatos da multiplicação na primeira tentativa, e isso pode levar ao medo da tabuada.
A maneira mais simples de começar a ensinar multiplicação é ancorar o conceito em termos de sua relação com a adição – uma operação com a qual seus alunos já devem estar familiarizados.
Antes de prosseguir, certifique-se de que seus alunos compreendam o primeiro pilar da multiplicação: que é simplesmente uma adição repetida.
Use exemplos relacionáveis, como o acima, para contextualizar esse fato.
Isso ajudará a escrever exemplos para que os alunos possam visualizar a ideia:
2 x 2 é o mesmo que 2 + 2
ou
3 x 4 é o mesmo que 4 + 4 + 4
2. Comece com os múltiplos de zero e um.
Multiplicando por zero: a propriedade zero
Destaque para sua classe que adicionar zero a um número não tem efeito sobre sua identidade:
n + 0 = n
Em seguida, explique que na multiplicação, qualquer número multiplicado por zero também é zero:
n x 0 = 0
Incentive os alunos a descobrirem exemplos da propriedade zero na sala. Por exemplo, uma sala de aula com 25 cadeiras com nenhum macaco sentado em cada uma significa que não há macacos na sala de aula. Opcionalmente, um exemplo divertido de uma atividade matemática divertida para entreter seus alunos envolve pensar em exemplos engraçados dessa propriedade, como 0 x um milhão = 0… ou … 0 x sanduíche de presunto = 0.
Multiplicando por um: a propriedade de identidade
Em suma, a propriedade de identidade afirma que o produto de um determinado número por um é o próprio número:
n x 1 = n.
Assim como com a propriedade zero, destaque para sua classe que multiplicar um número por um resulta no mesmo valor.
Para basear a propriedade em um contexto da vida real, incentive sua classe a pensar em instâncias da propriedade de identidade na sala de aula.
Por exemplo,
Um grupo de oito mesas é oito mesas
Uma única linha no calendário mostrando sete dias é sete dias
3. Cubra a tabuada, começando com os números “fáceis”.
Para revisar, seus alunos agora devem entender que a multiplicação pode ser considerada uma adição repetida.
Eles também deveriam ter levado algum tempo para multiplicar os números por zero e um. Embora não precisem conhecer os termos técnicos, os alunos devem entender como funcionam as propriedades zero e identidade.
Agora é hora de dar um dos maiores saltos: cobrir a tabuada.
Uma abordagem eficaz funciona da seguinte maneira:
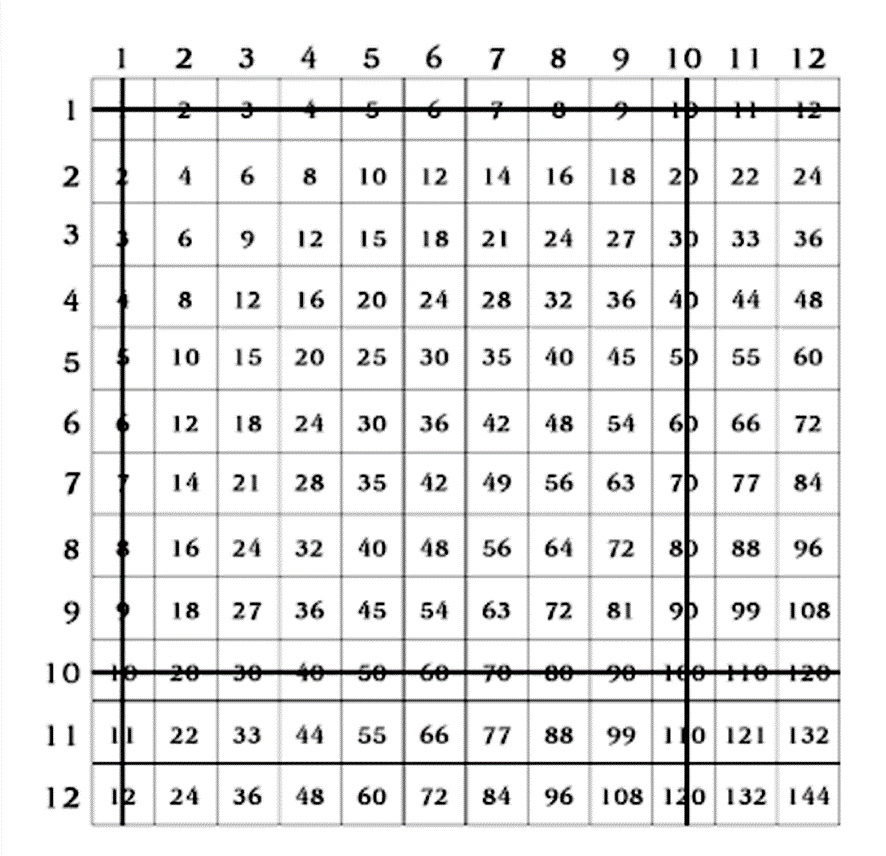
Mostre um gráfico ou slide retroprojeção da tabuada de multiplicação 12 x 12. Se desejar, complemente isso com cópias do gráfico de multiplicação para os alunos. Se um gráfico de 12 x 12 parecer muito complicado, execute o mesmo processo com um gráfico de multiplicação de 10 x 10.
Ensine os alunos a usar o gráfico e encontrar produtos seguindo e combinando a posição dos números usando os eixos vertical e horizontal.
Agora, fale sobre alguns dos padrões que você pode encontrar no gráfico. Ofereça pistas ou dicas aos alunos. Por exemplo, observe como todo múltiplo de dez termina em zero e todo múltiplo de cinco termina em zero ou cinco.
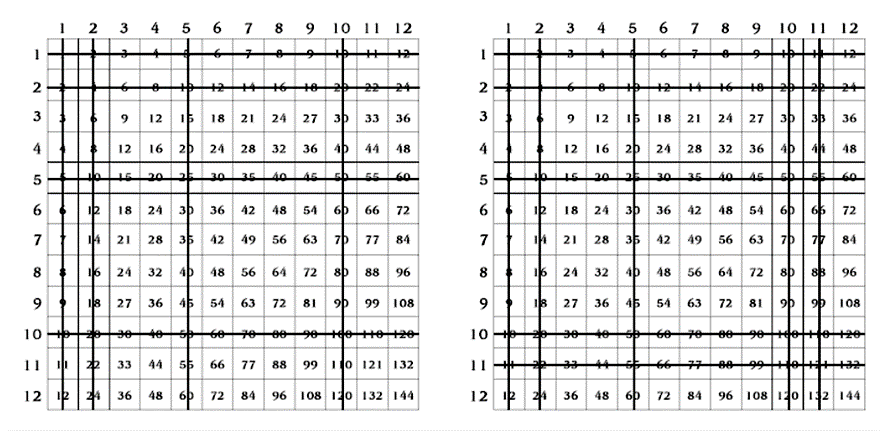
Pergunte aos alunos quais fatos são mais fáceis. Por exemplo, unidades e dezenas são fáceis. Agora que você discutiu os fatos de multiplicação “fáceis” – e o que os torna fáceis – elimine-os do gráfico.
Os alunos geralmente concordam que os dois, os cinco e os onze também são fáceis. Continue cruzando os números “fáceis” até chegar a um estágio que se parece com isto:
Veja os números restantes com sua classe. Use a oportunidade para conduzir uma discussão dinâmica e levar para a próxima etapa.
4. Mostre como a propriedade comutativa torna as coisas mais fáceis.
Assim como a adição, a multiplicação é comutativa, o que significa que a ordem dos fatores não altera o produto (a resposta).
Em outras palavras, dois números podem ser multiplicados em qualquer ordem e o produto será o mesmo. Por exemplo, multiplicar 8 x 2 dará a você a mesma resposta que multiplicar 2 x 8.
Quando você comunica isso de forma eficaz, isso encoraja seus alunos.
Mostre a seus alunos que cada resposta se repete, então eles só terão que aprender metade das tabelas restantes. Por exemplo, explique que aprender 3 x 6 é o mesmo que aprender 6 x 3!
Se os alunos já aprenderam as famílias de fato de 0-3, então eles também sabem quatro números cada um de 4-10.
Para reforçar ainda mais a propriedade comutativa, você também pode usar um modelo visual como o acima e apontar como os blocos amarelos estão dispostos.
Pergunte a seus alunos: “Esses dois arranjos não são iguais, mas apenas versões diferentes um do outro? Se contarmos o número total de unidades, eles são iguais?”
Ajudar os alunos a compreender essa propriedade é uma parte fundamental do ensino de multiplicação. Para que os alunos façam sozinhos e aprendam por meio da experiência direta, peça que sua classe crie modelos para ilustrar essa ideia e prove que a x b resulta no mesmo produto que b x a.
5. Divida a memorização em etapas fáceis.
Neste ponto, seus alunos estão prontos para começar a memorizar a tabuada. É provável que já o tenham começado.
Esteja ciente de que nem sempre é óbvio para os alunos porque eles precisam decorar os fatos da multiplicação. Comunique a importância de compreender o significado por trás dos fatos de multiplicação e como eles podem ser usados em situações cotidianas.
Embora existam muitas abordagens para memorizar o gráfico de multiplicação, lembre-se dos exemplos acima – os números “fáceis” – como um bom ponto de partida. Ao continuar sua lição, considere seguir estas regras:
Incentive os alunos e estabeleça um tempo para eles praticarem verbalmente ou por escrito.
Introduza novos fatos de multiplicação um por um, gradualmente para as etapas mais avançadas de multiplicação por 2, 3, 4 e assim por diante.
Dê aos alunos tempo para praticar os fatos de multiplicação. Encontre um ritmo que funcione bem em sua sala de aula. Se desejar, aproveite a aprendizagem entre pares para alunos com dificuldades.
Memorize os fatos em uma ordem estratégica. Assim que seus alunos dominarem 0-3, prossiga para 4-7 e, em seguida, 8-10. Dependendo de sua preferência, você também pode cobrir 11 e 12. Incluir problemas mais desafiadores como bônus o ajudará a avaliar os alunos de alto desempenho. Alguns professores incluirão alguns problemas mais difíceis como bônus ou para identificar alunos com alto desempenho.
Para ajudar na memorização, mantenha materiais visuais disponíveis em sua sala de aula. Não importa quantas vezes você cubra a multiplicação, é sempre uma boa ideia ter uma cópia física da tabela disponível em sua sala de aula.
Se você já tem um pôster, considere obter outros materiais que o ajudem a explicar a função da multiplicação visualmente.
6. Apresente as propriedades associativas e distributivas.
Embora esses conceitos sejam mais avançados, é importante que seus alunos os compreendam. Você descobrirá que eles podem fazer maravilhas para melhorar a matemática mental de seus alunos.
Observação: use o seu critério ao apresentar as propriedades abaixo. Eles não podem ser aplicáveis a alunos em qualquer ano inferior ao 4º ano.
A propriedade associativa
A regra da propriedade associativa afirma que, independentemente da forma como você agrupa os fatores, o produto será sempre o mesmo.
Por exemplo,
(a x b) x c = a x (b x c)
ou
(1 x 2) x 3 = 1 x (2 x 3)
Seus alunos podem entender esse conceito relacionando-o com a adição de colunas, por meio da qual eles agrupam adendos para encontrar a soma.
Os alunos também podem aprender a agrupar fatores da maneira que acharem mais conveniente enquanto procuram a resposta. Você pode explicar esta regra como uma extensão da propriedade comutativa acima.
A propriedade distributiva.
A propriedade distributiva é simbolizada como a (b + c) = (ab) + (ac)
Isso pode parecer complicado para os alunos, mas frequentemente eles já estão usando a propriedade por conta própria como um truque de matemática mental para resolver fatos de multiplicação mais desafiadores.
Simplificando, os spreads de propriedade para fora – ou, como o próprio nome indica, distribui o valor de uma igualmente a b e c.
Por exemplo, para 6 x 8, eles podem usar a propriedade distributiva para pensar: (6 x 5) + (6 x 3), ou 30 +18
Para explicar a propriedade para alunos visuais ou táteis, permita que as crianças explorem a propriedade distributiva com materiais como xícaras e feijões ou papel quadriculado.
Amostra
Quer compartilhar? Compartilhe o link.
Obrigada♥
Habilidades da BNCC:
(EF04MA11) Identificar regularidades em sequências numéricas compostas por múltiplos de um número natural.